大模型算力推演优化实战

阅读帮助

第一部分为看清：大模型的训练及推理过程是如何的，以及内部逻辑

第二部分为理解：大模型的训练及推理和算力的关系

第三部分为推演：用简单的公式量化大模型算力的需求

第四部分为优化：我们如何提高算力利用率

一、看清

1.1 大模型训练

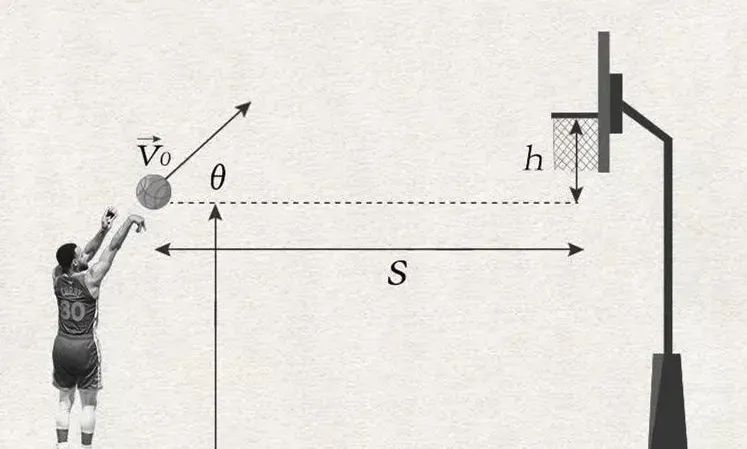
我们以投篮训练为例，来尝试理解大模型的训练过程。

假设你正在练习投篮，目标是投进篮筐。已知的是投篮和你的出手点高度、投篮角度、手腕力度大小有关，作为一个小白你并不知道出手点高度、投篮角度、手腕力度大小该控制多少，那么你的第一次出手就是一个随机控制，至于篮球进不进篮筐就交给上帝吧。

有一种可能是你进了，那么恭喜你，天才选手；但现实往往很骨感，你不但没有中而且距离篮筐还很远。聪明的你就开始分析你观察箭偏离篮筐的方向和距离，然后找出如何调整你的出手点高度、投篮角度、手腕力度大小等因素，以便下次投篮更接近篮筐。

第二次投篮就根据第一次的分析结果，调整了出手点、高度等，你发现这次距离篮筐更近了，但是还有优化的空间，以此类推直到第 N 次，你发现几乎可以百发百中了。

我们来看大模型训练包含哪几部分，以及和投篮训练的过程类比：

1、前向传播（forward pass）：在前向传播过程中，输入数据（例如图像、文本等）通过神经网络的各层进行传递，直到得到输出结果。这个过程包括了将输入数据与权重矩阵相乘、应用激活函数等操作。前向传播的目的是计算网络的预测输出，并将其与实际目标值进行比较，从而计算损失函数（loss function）的值。

以上述投篮类比：根据你目前的技能（神经网络的权重）来投篮，然后观察篮球距离篮筐的位置（神经网络的输出）。这个过程告诉你，根据你现有的技能，你的投篮表现如何。

2、反向传播（backward pass）：反向传播是一种高效计算梯度的算法。在这个过程中，损失函数关于每个权重的梯度（偏导数）被计算出来。从输出层开始，沿着网络的层次结构向输入层反向传播，计算每个权重的梯度。这些梯度表示了权重对损失函数的贡献大小，因此可以用于指导权重更新。

以上述投篮类比：这就像你分析篮球距离篮筐的位置，并找出如何改进你的投篮技巧。你观察篮球偏离篮筐的方向和距离（损失函数），然后找出如何调整你的投篮姿势、力量等因素（权重梯度），以便下次投篮更接近篮筐。这个过程涉及到计算梯度（找出如何调整技巧）。

3、权重更新（weight update）：在计算出所有权重的梯度后，我们使用优化算法（如随机梯度下降（SGD）、Adam 等）来更新权重。这个过程中，权重会根据它们的梯度值进行调整，以减小损失函数的值。这样，模型就能逐渐学习到从输入数据中预测目标值的能力。

以上述投篮类比：你经过分析找出如何调整你的投篮姿势、力量等因素（权重梯度），以便下次投篮更接近篮筐。这个过程涉及到更新权重（实际调整技巧）。

下面举例一个简单三层神经网络模型的推导过程

神经网络介绍见下图，包含三层：输入层、隐含层、输出层，以及每层的神经元及相互之间权重，目标是使得输入数据 x1,x2(0.05 和 0.05)，使输出尽可能与原始输出 y1,y2(0.25 和 0.15)接近。

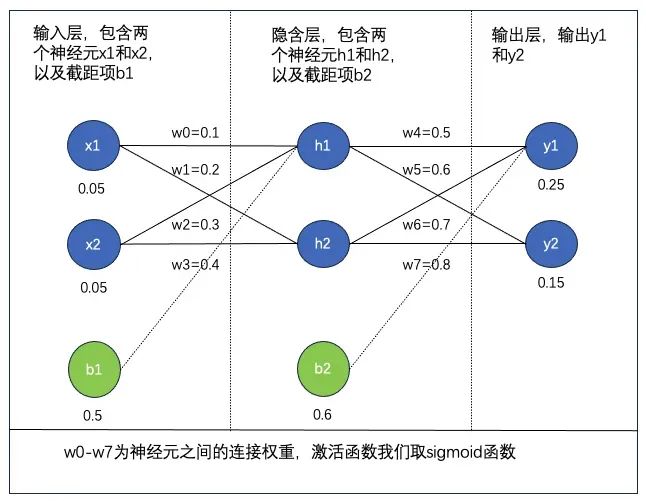
第一步：前向传播

1、输入层–>>隐含层

计算神经元 h1 的加权和：

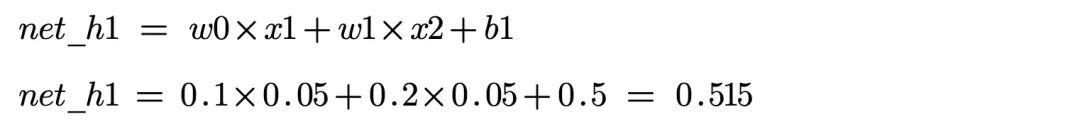
神经元 h1 的输出 out_h1：

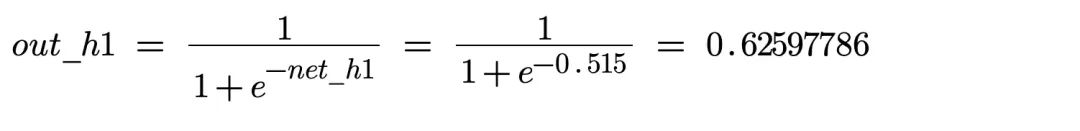
同理，可计算出：out_h2 = 0.63064853

2、隐含层–>>输出层

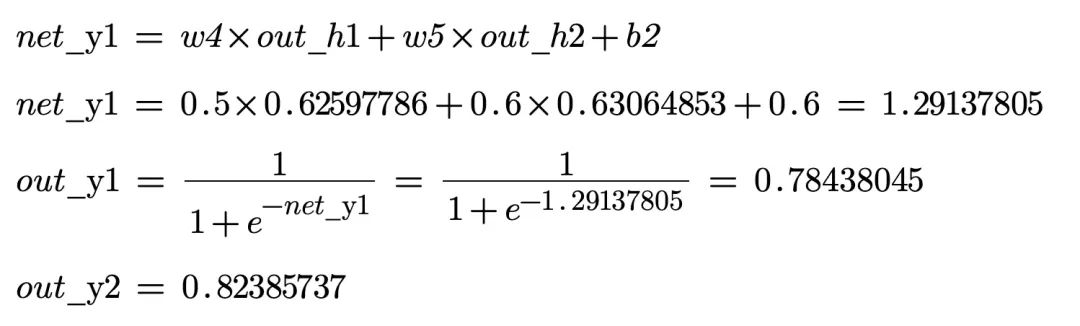
一次前向传播就完成了，我们得到输出结果[0.78438045,0.82385737] 与目标值[0.25,0.15]相差还很远，下面进行反向传播，更新权重值

第二步：反向传播

1、计算损失函数（Loss）

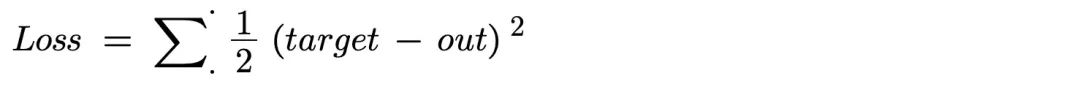
分别计算 y1 和 y2 的误差，总误差为两者之和。

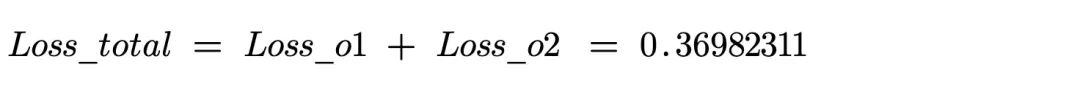
2、隐含层 –>> 输出层权值(w4-w7)更新

w4 对整体误差产生的影响，可以由偏导求出：

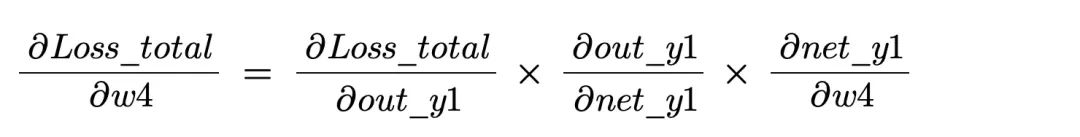
基于链式法则我们推出偏导可以拆分为三个子公式得到

第一部分

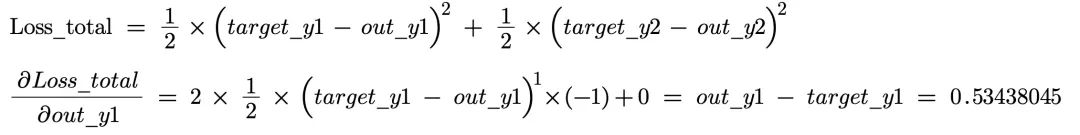
第二部分

enter image description here

第三部分

最后可以得出我们需要的偏导：

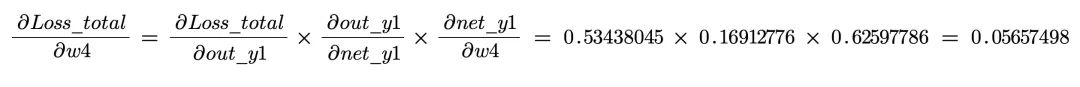
有了偏导数据，我们就可以更新 w4 的值：

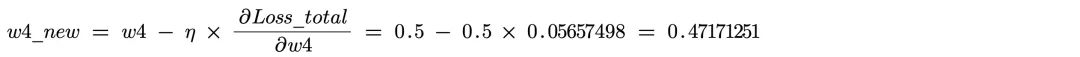
同理可以计算 w5-w7 的更新值：

w5’=0.57150144

w6’=0.66939351

w7’=0.76916515

3、隐含层 –>> 隐含层权值(w0-w3)更新

方法和上面类似，我们先推算下 w0 的更新值：

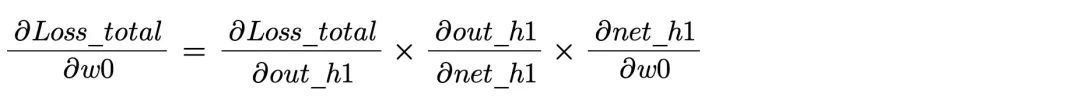
第一部分

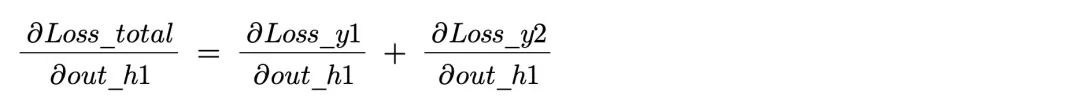
根据之前的计算结果：

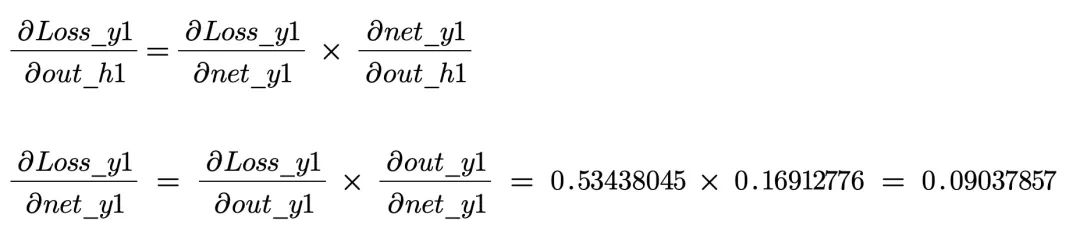
同理可以计算出：

这样就可以得出：

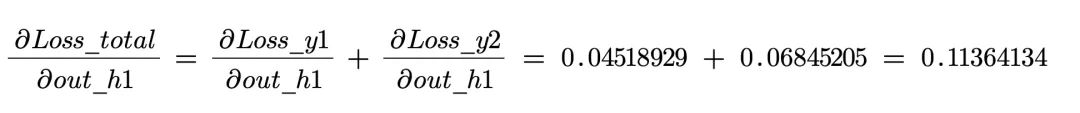
第二部分

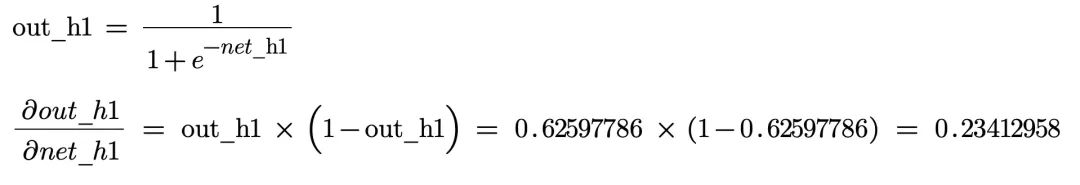
第三部分

综上三部分，我们可以计算出：

最后，通过偏导来更新 w0 的值：

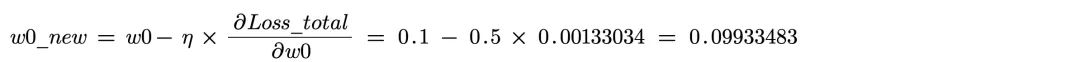
同理可以计算 w1-w3 的更新值：

w1’=0.19933483

w2’=0.29922866

w3’=0.39922866

这样一次反向传播就完成了，我们再把更新的权重重新计算，不停的进行迭代，迭代一次 Loss 值由 0.36982311 -> 0.36277389，以此类推，当迭代次数足够大，Loss 值不断变小。

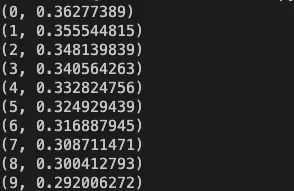
enter image description here

1000 次迭代后，Loss 值已经很小了：

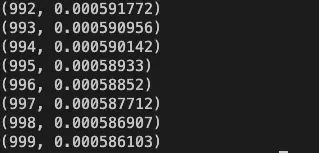
1.2 大模型推理

有了一个训练好的模型，我们就可以进行推理上线了，推理过程主要包括五个步骤：

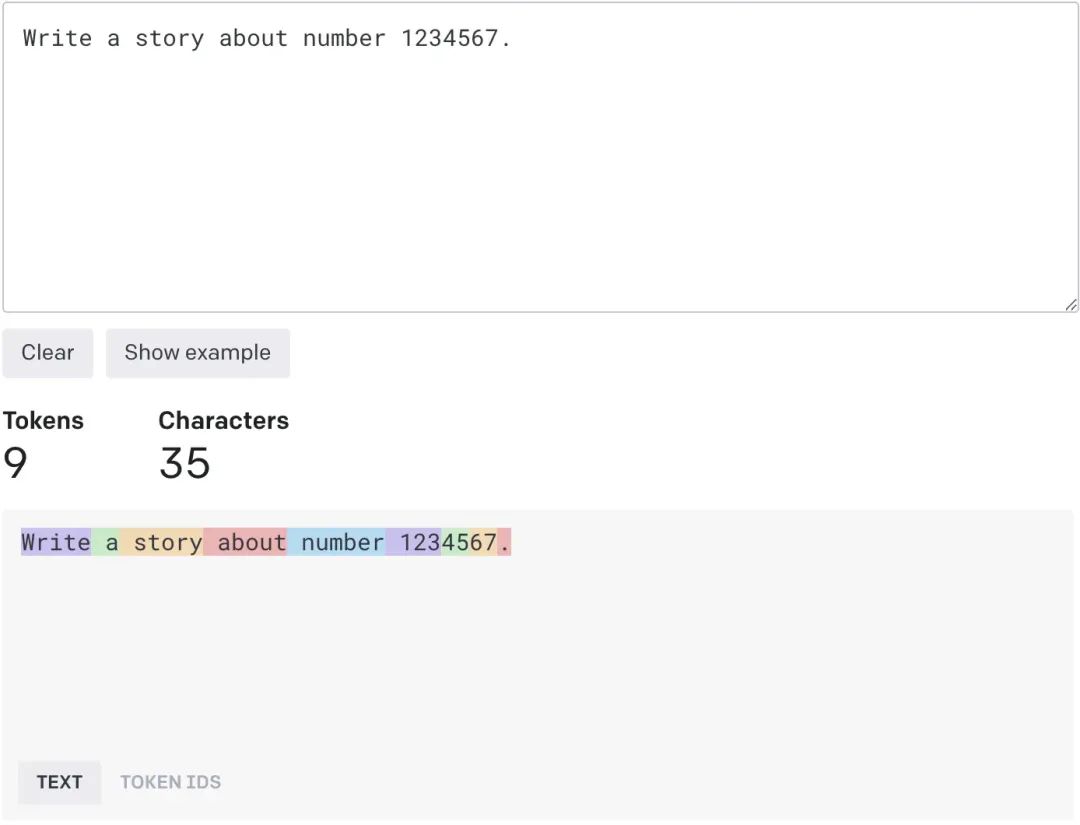
第一步：分词（Tokenize）将输入的文本分解为更小的 token，这些部分可以是单个单词，字符等，简单理解为类似一种编码算法，把字符映射到 ID。比如下面这句 [Write a story about number 1234567.]就可以映射到一串数字[16594, 257, 1621, 546, 1271, 17031, 2231, 3134, 13]

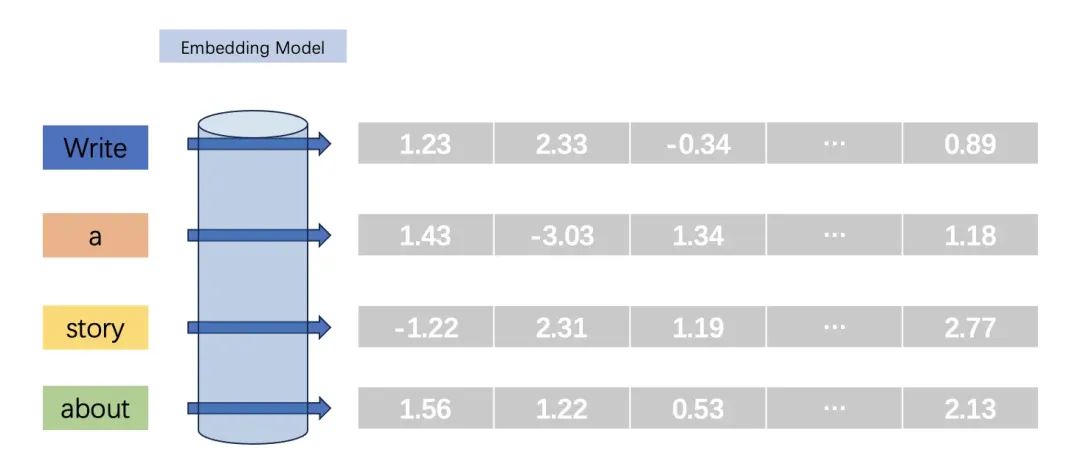
第二步：嵌入（Embedding）将高维度的数据（例如文字、图片、音频）映射到低维度空间的过程，最终以多维度向量表示每一个 object（大模型就是指的每一个 token）。

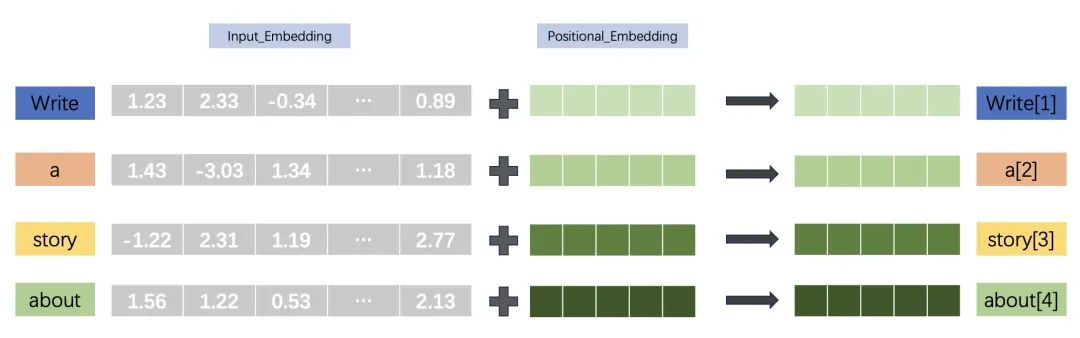
第三步：位置编码（Positional Encoding）将 token 在句子中的位置信息进行编码，使得输入 Input = Input_Embedding + Positional_Enbedding 增加位置信息。

至于为何要增加位置编码，互联网上有很多大佬解释，这里不赘述，简单归因两点：

1、神经网络 RNN 本身是按照序列顺序处理句子的，Transformer 模型用 Attention 取代了 RNN ，它对数据的处理是同时并行处理，不包含时序信息

2、时序不同的句子含义会有很大不同

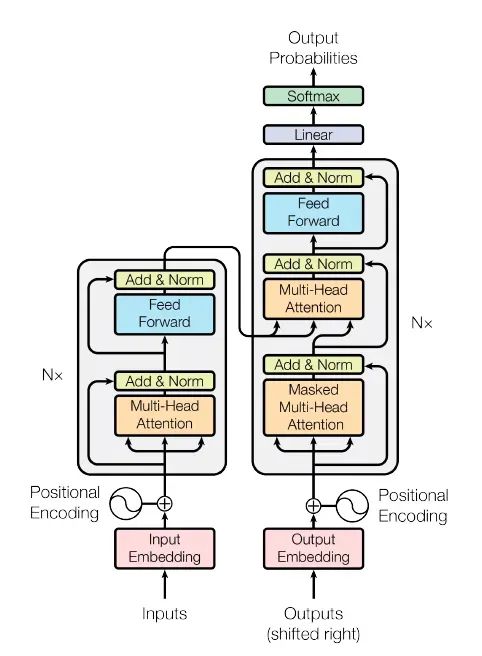
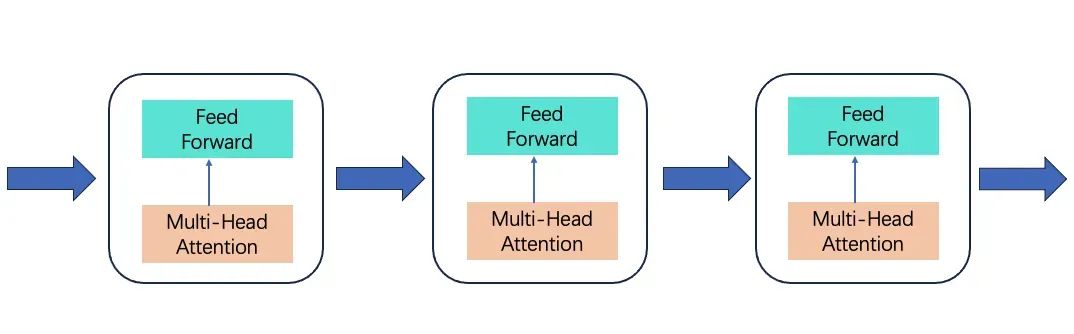
第四步：Transformer 层 将处理后的 Input 输入神经网络 +attention 注意力模型进行处理：

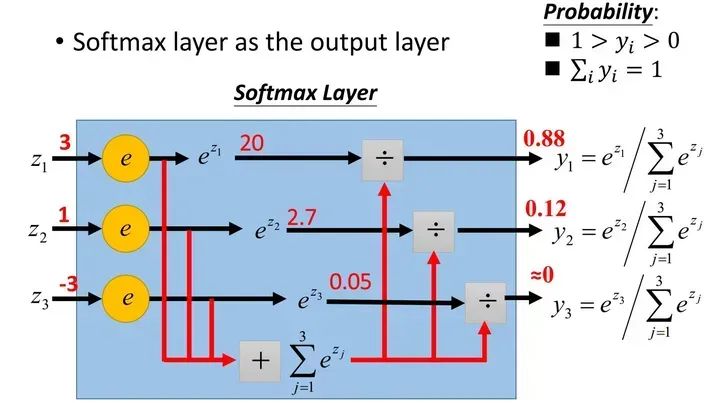
第五步：Softmax 将多个神经元的输出映射到（0,1）区间，进而转换为一组概率分布（加和为 1）（convert the decoder output to predicted next-token probabilities）

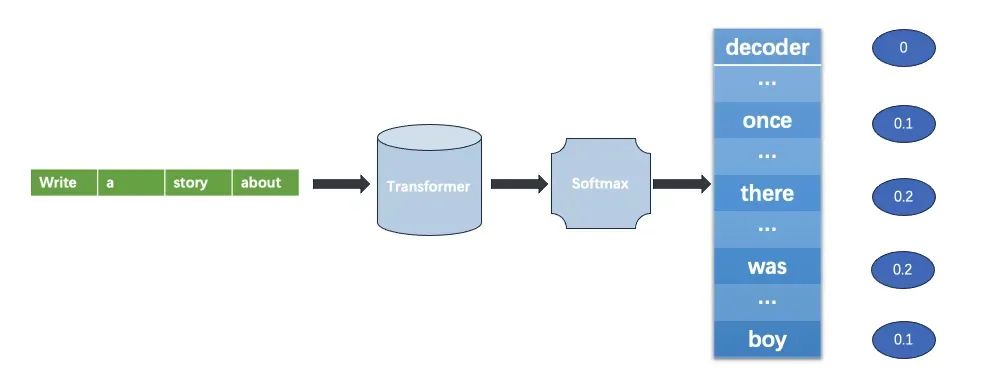
示例一次计算过程如下：

二、理解

2.1 训练过程

第一章节第一小节讲述了大模型的通用过程，包括前向传播（forward pass）和反向传播（backward pass），我们以单位计算 unit 来计数，一次前向传播为 1 unit，一次反向传播为 2 unit（因为这里需要计算一份输出的梯度+参数的梯度），那么一次完整的训练包含了 1+2 = 3 unit，也就是对于每个 token、每个模型参数，需要3 unit 的计算。

每一个 unit 的计算都是矩阵运算，我们知道对于一次矩阵运算需要进行一次乘法及加法，共计 2 次浮点运算。

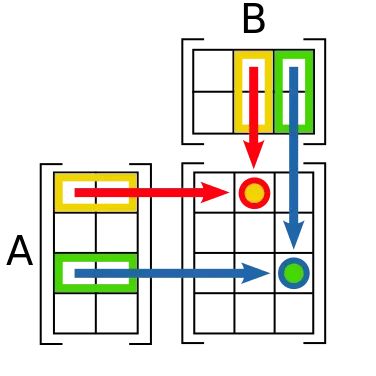
综上两部分，我们可以得出对于每个 token、每个模型参数，需要进行 3 unit × 2 flops = 6 次浮点运算。

补充：训练还有一个可选流程激活重计算技术（本质上是时间换空间），使用激活重计算技术来减少中间激活显存需要进行 1 次额外的前向传播，如果使用重计算技术，那么对于每个 token、每个模型参数，需要进行 4 unit × 2 flops = 8 次浮点运算。

2.2 推理过程

第一章节第一小节讲述了大模型的推理过程，主要计算量在 Transformer 解码层，这一层对于每个 token、每个模型参数是一个单位 unit 的计算量，所以推理过程每个 token、每个模型参数，需要进行 1 unit × 2 flops = 2 次浮点运算。

三、推演

有了如上的两个章节的分析，我们可以得出一个比较通用的算力评估，所需的 FLOPs 浮点运算量：

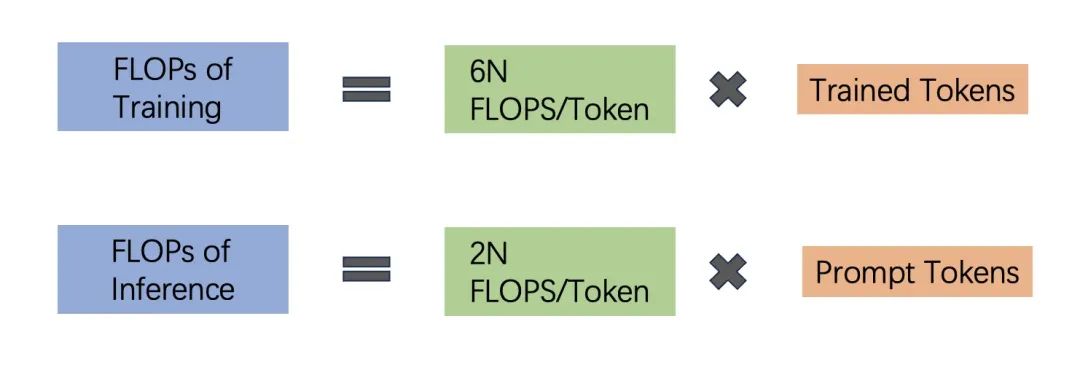
3.1 算力底座

得到通用的计算量评估，我们需要进一步细化到我们熟知的 GPU 卡算力上，为此我们需要一些算力底座的相关信息，一些常用 GPU 卡对比的信息如下：

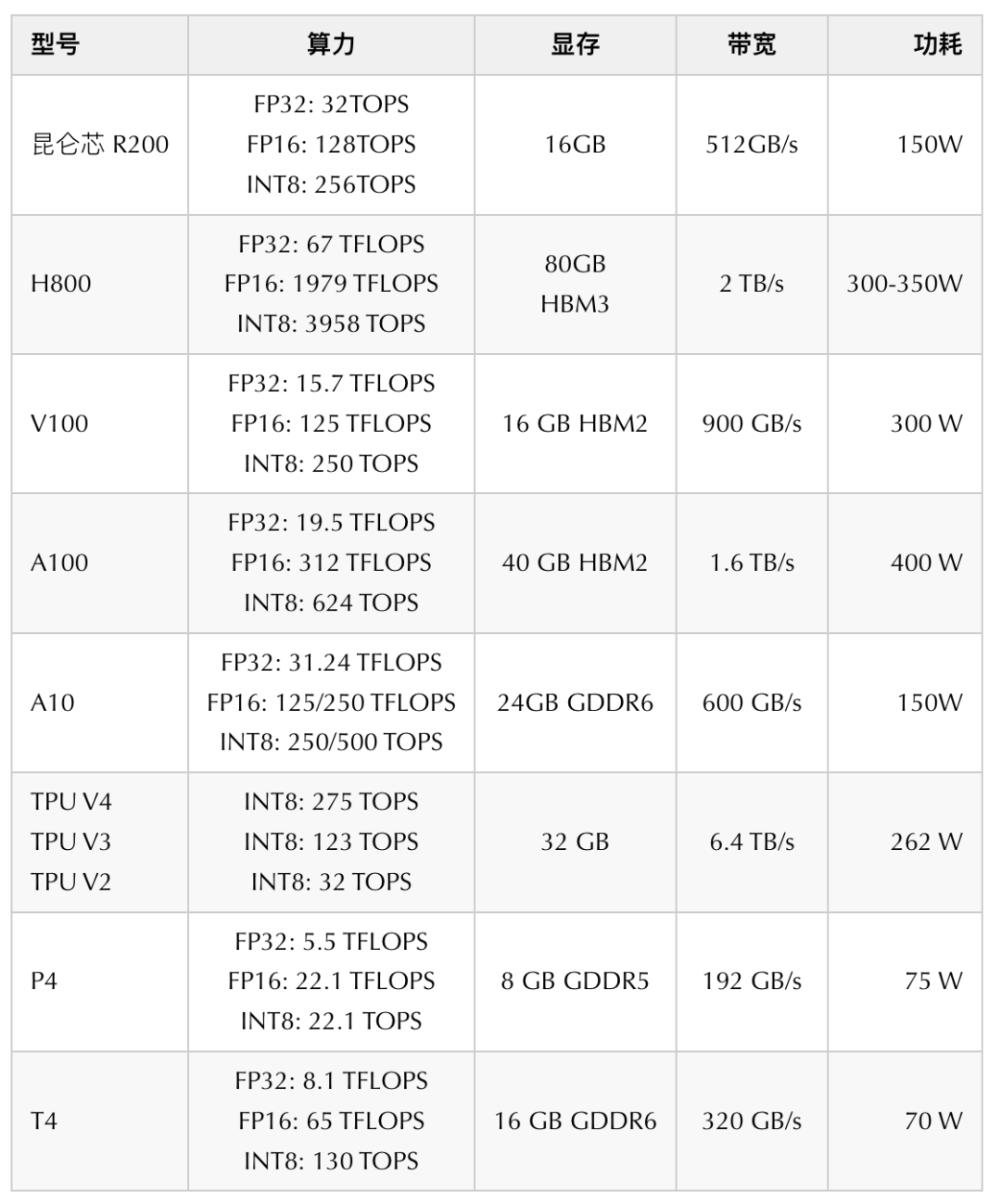
3.2 算力评估

有了通用的 GPU 卡的算力信息，我们就有了可以评估所需 GPU 卡数量的依据，在上述通用算力评估的基础上，我们就有了基于 GPU 卡的算力评估：

其中 FLOPS utilization 以目前业界能达到的最大值来进行推测：

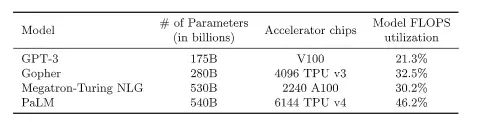
感兴趣可查阅 PaLM: Scaling Language Modeling with Pathways

3.3 算力验证

以业界开源大模型为例，我们通过公式计算算力基本和公开数据一致，以下两个维度来推算：

3.3.1、需要的算力

例如 GPT3 参数规模 175B，训练 token300B，采用的是稠密（Dense）模型，按照公式计算 6 × 175B × 300B = 3.15e23 FLOPs 公开的 GPT3 运算量 3.1e23 FLOPs，二者基本一致。

除此之外，该算力模型对于公司内部的一些大模型评估也是适用的，业务敏感信息这里不展示具体数据了。

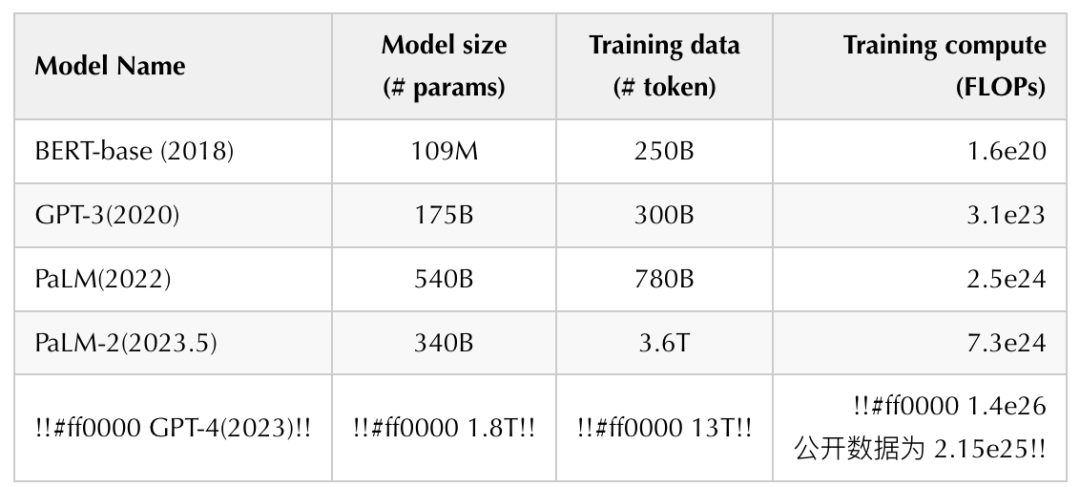
标记红色的为 7 月 11 号最新公开的 GPT-4 的核心数据，大家可能会注意到，GPT-4 好像并不符合算力公式，这是不是说我们的公式存在一些逻辑错误呢？那么我们就深入探讨下 GPT-4 的训练过程：

GPT-4 采用了混合专家（MoE）模型

专家混合模型（Mixture-of-Experts，MoE）：MoE 模型是一种深度学习架构，该架构，通常由多个专家（Experts）组成，每个专家负责处理输入数据的不同方面，并拥有自己的参数集（也有一些参数，例如 embedding，可以被所有专家共享，即共享参数）。在模型的推理过程中，根据输入数据的不同特征，模型会将输入路由到不同的专家，每个专家根据其参数集处理对应分配到的输入后完成输出，最终输出则是各个专家输出的集成。

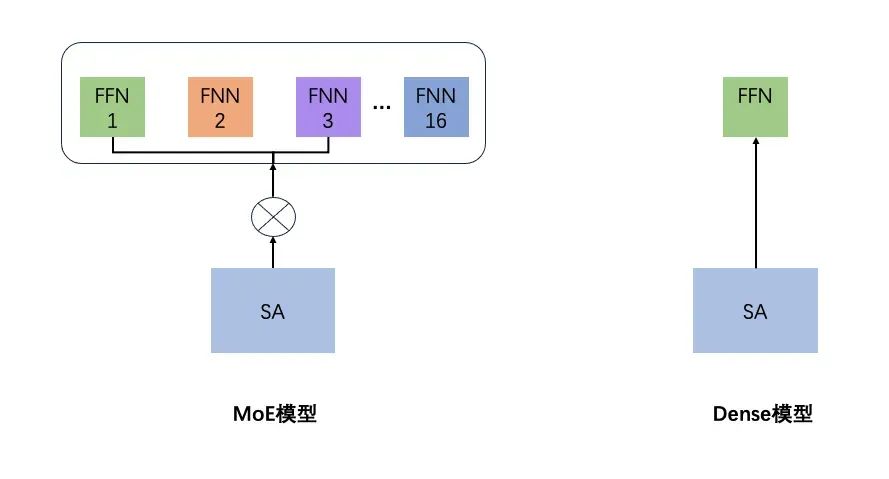
如上图，简单理解 MoE 类比：我把百度拆分为了，医学知识百度+历史知识百度+地理知识百度等等，实际我请求百度的时候，百度路由到对应的 XX 知识百度上，然后回答我的问题。

实际上 GPT-4 采用了 16 个专家，每个专家的 MLP 参数约为 1110 亿，每次前向传递有 2 个专家进行路由，还有 550 亿共享参数用于注意力机制，如上图每次调用实际走到了其中 16 个专家中的 2 个，大大减少了所需的训练以及推理计算量。

最后我们再回过头看下之前根据公式计算不匹配的问题，这里就会有一个问题就是实际执行的参数规模变化了：1.8T -> 1110 亿 * 2 + 550 亿，重新计算得到计算量为 6×2770 亿 ×13T=2.16e25 与公开 2.15e25 基本一致。

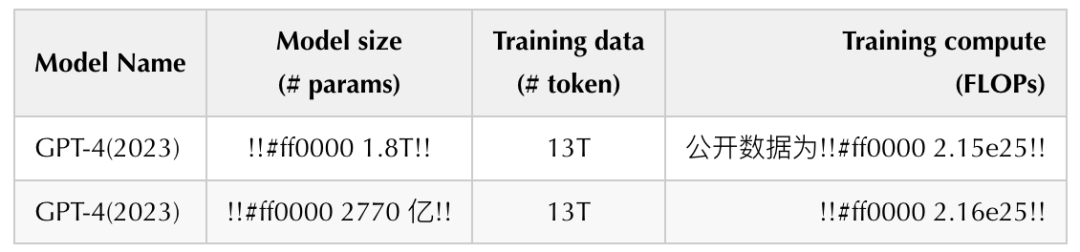
^^注：1T = 1000B = 10000 亿^^

3.3.2、需要的 GPU 卡/时

例如 GPT3 参数规模 175B，训练 token300B，采用的是稠密（Dense）模型，按照下图公式计算：

分子为训练所需要的浮点运算量：1750 亿（参数规模） × 6 × 3000 亿（token 量）；

分母为 312TFLOPS（一张 A100 FP16 精度下的算力） × 46.2%（利用率）× 3600 （1 小时对应的秒）

得到的结果就是60.67 万 A100/小时 = 2.53 万 A100/天，如果是 1000 张 A100，需要的训练时间约为一个月，和公开的数据也基本一致

再说到 GPT4 参数规模 1.8T，训练 token 13T，采用的是稀疏（MoE）模型，按照下图公式计算：

53433642 A100/小时 = 2226402 A100/天，如果用 25000 张 A100 训练，需要 89 天；与公开数据使用了约 25000 个 A100 进行了 90-100 天的训练基本一致

3.3.3、业界模型推演

有了如上的验证，我们推演下业界一些公开模型的算力数据：

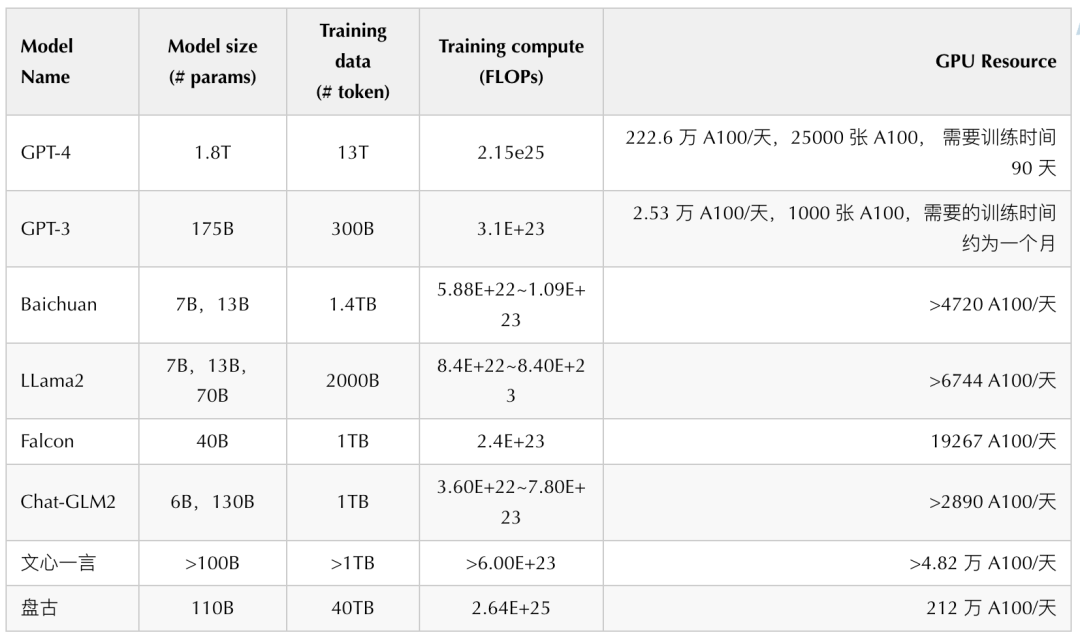
四、优化

至此，所有的算力推演部分结束，下面我们来简单看一组数据

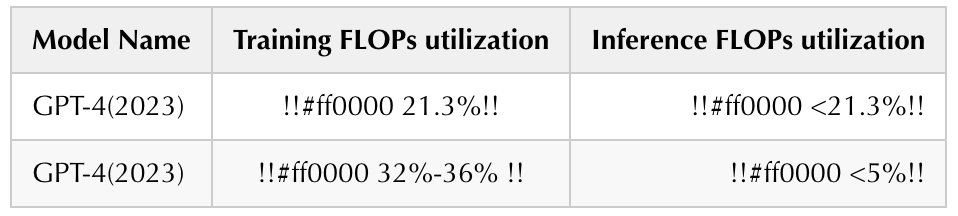
由上图可以看到，不论是训练还是推理，利用率都不是特别高，这其实对于大规模的模型推广是一大阻碍：

1、成本阻碍

我们第三章公式，采用 AWS 最具成本效益的 GPU 选择，拥有 8 个 A100 实例的有效时薪 19.22 美元；估计其成本约为 0.0035 美元/1000 token，OpenAI 的 API 定价为 0.02 美元/1000 token，
其毛利率约为 80%；假如利用率提升 10%，单位成本就可以降低 30%以上

2、算力阻碍

目前已知的各大互联网公司都在囤卡，寻求抓住大模型的机遇，所以能得到多少张 GPU 卡也存在一定的不确定性；如何能够高效利用 GPU 也可以反向推动项目的进展，从另一个角度破除算力瓶颈’卡脖子’

优化分析的一些现状：

1、基础工具

英伟达提供了 Nsight System（nsys）工具查看模型运行时的 CPU/GPU 执行情况，可以帮助发现 GPU 运行时的一些问题

2、训练过程

大模型训练中存在几种经典的分布式并行范式，分别为数据并行（Data Parallelism），流水线并行（Pipeline Parallelism）和张量并行（Tensor Parallesim）。

2.1 数据并行：ZeRO 优化器

ZeRO（Zero Redundancy Optimizer）思想就是拆分 参数、梯度及优化器状态，使得节点保存部分参数、梯度及优化器状态

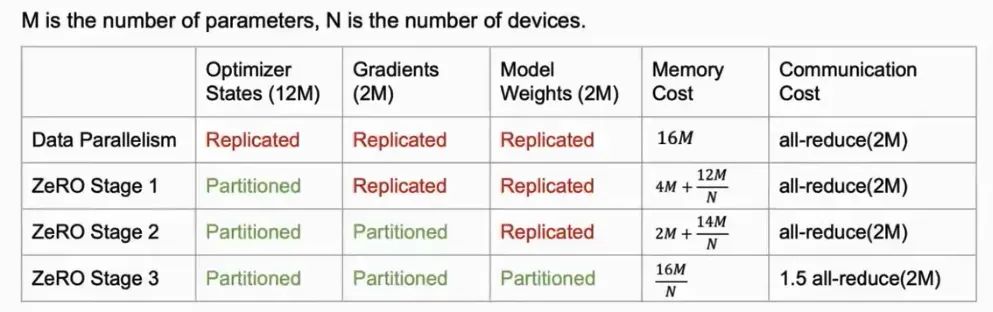
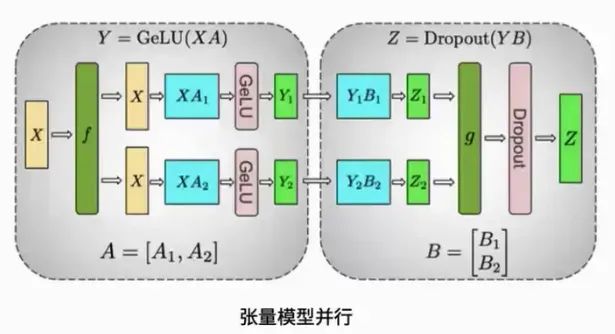
2.2 模型并行：张量并行和流水线并行

• 张量并行 ：将模型中的线性层切分到多个显卡上，并插入适当的 All-reduce 算子实现数据同步（通信量大）

• 流水线并行 ：将模型分为多个 stage，放置在不同的显卡上计算

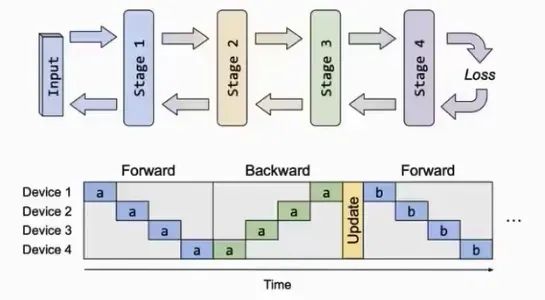
3、推理过程

像一些公司进行了模型的 CPU 和 GPU 运算部分拆分，单独部署成 CPU/GPU 微服务，减少 CPU 和 GPU 之间的相互干扰，以此提升性能。

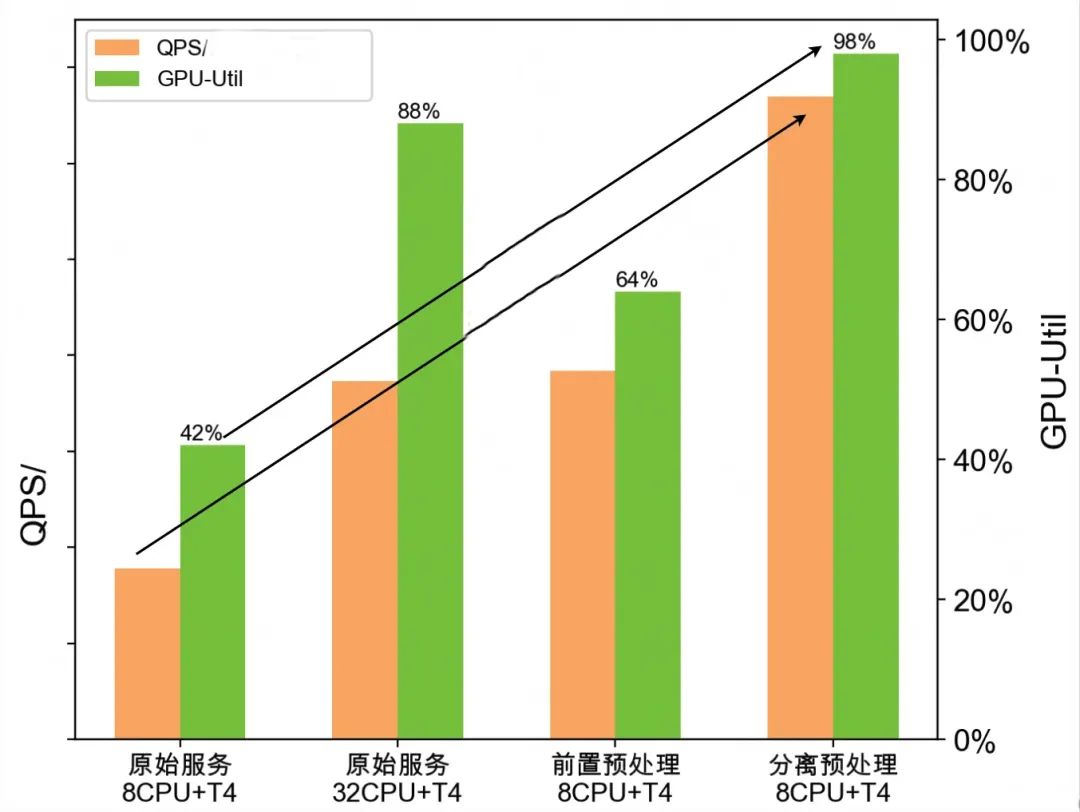
目前对于这部分还是知之甚少，后续会对于这部分再单独展开，欢迎有兴趣的小伙伴一起探讨。

结束语

随着混元的落地，LLama2 的开源，会有更多的预训练模型和推理模型的资源利用优化、评估的事情，这也是我们下阶段工作（算力评估、性能优化）的一个开端，欢迎对大模型算力及优化感兴趣的同学一起交流沟通！

作者：zhenfei